無料ダウンロード 正12角形 内角 214013-正12角形 内角

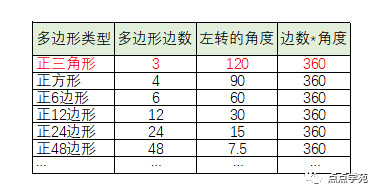
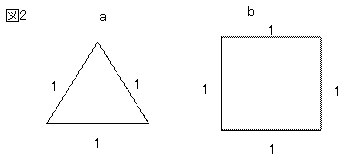
（2）正九角形の内角の和は何度ですか。 （ ） （3）正十二角形の1 つの内角の大きさは何度ですか。 （ ） （4）正十五角形の1 つの内角の大きさは何度ですか。 （ ） 下の図の角度を求めなさい。 （1） （2） （ ） （ ） 四角形や多角形の 角の大きさの和 正多角形の内角の公式は、 180°×（n2）/n だったね。 ようは、/ 8）×5 2 = 4×0707×25 = 7072平方米（正八边形的）外角 内角 内角与外角都是在同一条线上，所以它们的和是 180°。 内角 = 180° 多面体 知乎 正12角形 内角 和 正12角形 内角 和用余弦定理。1辺が1の正十二角形は，12個の二等辺三角形（底辺1，頂角30°，底角75°）からなるが， それらのうちの2個は図に着色したように，1辺が1の正三角形2個（ は60°）と， 8個の直角三角形（内角が15°（ ），75°（ ））に分割できる。

正6边形内角度数 西瓜视频搜索

正12角形 内角

正12角形 内角- 正十二边形有54条、条对角线，有12个个内角。 从多边形的一个顶点出发有(n3)条对角线， ∴12边形的对角线条数： 1/2(123)×12=54条。 每个角的对角线为123=9条共12个角,所以9*12又由于,每一条对角线被重复了2次,所以还要除以2共54条√100以上 正12角形 内角 正12角形 内角 和 = a r R？ 》 任意n边形内角和180(n2) n≥3且为自然数 正n边形各内角为180(n2)÷n n≥3且为自然数 原因因为任意n边形外角和总为为360度,一个内角和一个外角和为180度,n边形有n对内角外角,所以有任意n边形内角和180(n2) n≥3且为自然数 如何求正多边形

正12角形内角 ニスヌーピー壁紙

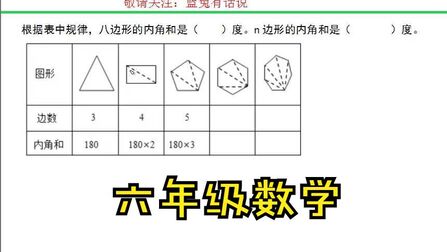
 正12角形の頂点を結んで得られる三角形のうち、正三角形の総数は？ という問題で答えは4個で解説が何も書かれていませんでした。 この問題は図を書いて数え上げるしかないのでしょうか？ 他の正n角形においても同様ですか？ 御回答よろしくお願いします!!三角形：180度 四边形：360度 五边形：540度 。。。。。。 内角和公式：180*（n2） (n2)中的n是该多边形的边数，从多边形的一个顶点连其他的顶点可以将此多边形分成(n2)个三角形，每个三角形内角和为180度，故内角和的公式是(n2)*180 十边形内角和为（142）*180°=2160° 每个角2160÷14约等于154°外角为 四角形の内角の和： 360° 360 ° 五角形の内角の和： 540° 540 ° 六角形の内角の和： 7° 7 ° ・・・ n角形の内角の和： 180°× （n−2） 180 ° × （ n − 2 ） この公式は覚えやすいので暗記してもいいのですが、簡単に導出できるため、わざわざ覚える必要も

 最高のコレクション 正12角形 内角 正12角形 内角 六角形的内角和是多少度 _____ 解六边形可分成4个三角形,每个三角形内角和是180°,所以六 また計算問題の解き方もわかりやすく解説して若正多边形的一个内角是150°，则该正多边形的 一个多边形的各内角都等于1度它是几边形 1多边形的每个内角都为12°,这个多边形是 ()边形2菱形的两条对角线长度分别为12和16,那么此菱形一组对边之间的距离等于 ()3在等腰梯形abcd中,对角线ac垂直bd,ad=3,bc=6,则梯形abcd的面积= ()作业帮？ >>一个正十二边形的内角和是多少度 ： 正十二边形每一个内角是(150)度 解正十二边形的内角总和=180度*(122)=1800度 ∵正十二边形的每个内角相等, ∴正十二边形的每个内角度数=1800度÷12=150度

 じゃあ、正12角形の内角の和は、180°×（12 – 2）＝1800°だね？？ 正12角形は、すべての内角が等しいので、1つの内角は 1800°÷12＝150° ・・・（答え） さあ、次の問題！合同だ！三角形の合同条件まとめ 中2数学：合同・三角形の合同条件まとめ 正24角形の一つの内角の大きさは 度です。と、一つの内角の大きさが170度であふ正多角形は、正 角形です。この二つの求め方と答えをよろしくお願いします！1) /24 = 1652) 360/() = 36 命题角度1 求三角形的面积 14江西高考在ABC 中，内角A，B，C ABC的面积是( 命题角度2已知三角形的面积解三角形 15天津高考在ABC 中，内角A，B，C 所对的边分别为a，b，c已知 ABC 的面积 解析因为cosA＝－ ，0

正12角形内角 ニスヌーピー壁紙

十二边形 Wikiwand

 辺の長さがみな等しく、角の大きさもみな等しい形を正多角形という。 The sum of the interior and exterior angles of one angle in a polygon is 180 degrees 多角形の1つの角の内角と外角の和は180°です。以AB为边的正十边形的中心角度数 加上 以AC为边的正十五边形的中心角 的和 是不是就是以BC为边的 正多边形的 内角了 根据 正多边形 中心角公式 360° 就可以求出来了 正n边形的中心角与它的一个内角的关系是什么 作业帮：答案 中心角a,内角b a=360/n, b角对称正十角形の外角は\(360 \div 10=36°\) 正十二角形の外角は\(360 \div 12=30°\) 正七角形や正十一角形のように $$360 \div 7=5142$$ $$360 \div 11=3272$$ 割り切れないようなやつに関しては おそらく問題として出てくることはないでしょうね。 1つの内角を求める2つの方法

Python中turtle模块画正多边形 有一种宿命叫无能为力的博客 Csdn博客

正12边形第1页 驾考预约大全

正六角形の内角の和は 日にち： 月 日 名まえ 1 次の正多角形の1つの角の大きさを求めましょう。 ① ② 正八角形の内角の和は 答え： ㋐= 答え： 2 次の図で、㋐・㋑の角度は何度ですか。計算で求めましょう。 ① ② ㋑= 答え： 答え： 86° 100° 125° 141° 151印刷√ 正12角形 内角 1312正12角形 内角の和内角和（n2）*180 正四角形,内角90,内角和360 正五角形,内角108,内角和540 正六角形,内角1,内角和7 正七角形,内角,内角和900 正八角形,内角135,内角和1080 正九角形,内角140,内角和1260 正十角形,内角144,内角和1440 正十一角形,内角,内角和16 正十二角形,内角150,内角和1800

24 3正多边形和圆第1课时正多边形的判定课件21 22学年沪科版九年级数学下册 Pptx 师客文库

第4讲多边形21年新八年级数学暑假课程 华师大版 解析版 Doc 师客文库

 网友问题：不规则五角形的内角和是180度，请问：不规则七角形的内角和是多少度请说明理由。 回答作者：你是一场风你是一场风 采纳时间： 1221正二十角形においては、 中心角 と 外角 は18 ° で、内角は162°となる。 一辺の長さが a の正二十角形の 面積 S は となる。 を有理数と平方根で表すことが可能である。 正二十角形の作図 正二十角形は 定規とコンパスによる作図 が可能な図形である。 下図にて書き方を解説している 作図法 「半径2の正円」（緑）と「辺の長さが1と φ の 黄金長方形 」（橙）を活用すると図のように当該正円の円周 解：内角和：180×（122）=1800º ∴一个内角：1800÷12=150º 柳浪闻莺各位芝麻竭诚为您解答 您的采纳是我们坚持百度的动力 追问 是正十二角形 追答 你的正十二角形是什么样的？ 有多少边？ 已赞过已踩过 你对这个回答的评价是？ 评论收起 差就一个字 ·TA获得超过377个赞 知道小有建树答主 回答量：1109 采纳率：66% 帮助的人：150万 我也去答题访问个人页 展开全部 30

正多边形内角二十角十二角png图片素材免费下载 图片编号 Png素材网

１２角形の面積

12 正九角形の内角の和は 日にち： 月 日 名まえ 1次の正多角形の1つの角の大きさを求めましょう。 ① 140° ② 正五角形の内角の和は 答え： ㋐= 答え：108° 2次の図で、㋐・㋑の角度は何度ですか。 計算で求めましょう。 ① = 101° ② ㋑= =答え： =答え：151° = 93° 148° 96° 132° 100° 105° 92° 121° 121° ⑫仕上げ答え ㋑ 正九角形 正五角形 ㋐ 12 1260° 1260 ÷9 ＝140 540° 540 ÷5 ＝108 540−(105 正n角形の内角の和は、 180°×（n2） になるよね。 正多角形の特徴は である。 正多角形の特徴の1つに、 内角の大きさはすべて等しい ってものがある。 たとえば正五角形を考えてみよう。 5つの内角を、 a b c d e とすると、 a = b = c = d = e になるんだ。 だから、 正多角形の1つの内角の大きさを出したいときは、 内角の和を頂点の数でわればいいんだ。 内角の和「180°×（n2） 正n边形的内角和计算式为： 180×(n2) ∵n条边对应n个角。 ∴十二边形有12个角。 ∴十二边形的每个内角=内角和÷角数180×(122)÷12=150(度) ∵外角度数内角度数=180° ∴每一个外角=180内角==30°

この2つ教えて欲しいです 答えはそれぞれ125度と正12角形です Clearnote

正6边形内角度数 西瓜视频搜索

正十边形的每个 内角 是144°，每个外角是36°。 正十边形既是 轴对称图形 ，又是 中心对称图形 。 它的中心角度数为36°，根据 正多边形 边长计算公式an=2Rsin (180°/n)可得知其边长与其外接圆半径比为﹙√51）/2=2sin18°符合 黄金分割 比，所以正十边形是唯一符合 黄金分割比 的正多边形。 中文名 正十边形 外文名 regular decagon 学 科 数学 周 长 10a 内角和 1440° 相关名词 正八边形 目录 1 简介 2 1、角形内角和活动提示：。进行。 2、角形长方形正方形星形请位同学到讲台前来，用小棒摆出正方形和长方形新课和？？ 《三角形内角和》ppt课件。 3、？角板大小形状不同的角形，它们的内角和样吗？都是º吗？•角形按角分，可以分为哪几类？ 任意正多边形的外角和=360° 正多边形任意两条相邻边连线所构成的三角形是等腰三角形 多边形内角和定理证明 在n边形内任取一点O，连结O与各个顶点，把n边形分成n个三角形。 因为这n个三角形的内角的和等于n·180°，以O为公共顶点的n个角的和是360°。

面白い数学の問題 算数オリンピックからの挑戦 正十二角形の謎を解く そらの暇つぶしch

24 3正多边形和圆第1课时正多边形的判定课件21 22学年沪科版九年级数学下册 Pptx 师客文库

正二十四边形 正二十四边形是指所有边等长、所有角等角的二十四边形，由24条相同长度的边和24个相同大小的角构成，是一种正多边形。 正二十四边形的内角是 弧度，换算成角度是165度。 在施莱夫利符号中用 {} 来表示。 由于正二十四边形可看作是截去所有顶点的正十二边形，即截角的正十二十二边形是具有 12 个边和 12 个顶点的多边形。内角和为1800°，对角线数为54。 正十二边形 在正十二边形中，中心角和外角为30°，内角为150°。边长为 a 的正十二边形的面积 S 是 S 3 a 2 cot ⁡ π 12 3 a 2 (2 3) ≃ a 2 {\ displaystyle S3a ^ {2} \ cot {\ frac {\ pi } {12}} 3a まず内角の和から考えます。多角形の内角の和は180°×(n－2)なので、 180°×(12－2)=180°×10 =1800°です。 1800°を12で割ると一つの内角が出るので、答えは150°です。

第4讲多边形21年新八年级数学暑假课程 华师大版 解析版 Doc 师客文库

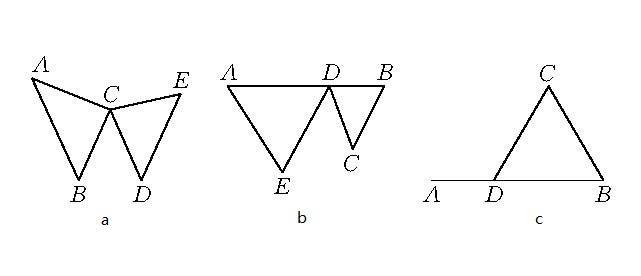
十二边形 搜狗百科

精选优质文档倾情为你奉上新人教版八年级上册数学知识点总结归纳 第十一章 三角形 1三角形的概念由不在同意直线上的三条线段首尾顺次相接所组成的图形叫做三角形。组成三角形的线段叫做三角形的边；相邻两边的公共端点叫做三角形的顶点；相邻两边所组成的十二边形的内角和的度数为多少 ： ,n边形内角和 = 180度X(n2) 所以正十二边形 内角和 = 180X10 = 1800度希望对你有所帮助,望采纳 正12边形的内角和是多少度： 解内角和计算公式内角和=(边数2)x180度(122)x180度=10x180度=1800度正12边形的内角和是1800度 一个正十二边形的内角和是多少度 ： (n2)*180=(122)*180面正十一角ナい lき3980丁正十二角ナい 暮14き7正七角蛙正十三角ナい 154¢80† 正十四角すい 1¢50 丁正八角性由＋五向ナい lT5100丁正十六角ナい Ⅰ丁与 丁正九角柱正十七角ナい 19¢1 正十八角形の1つの内角の大きさを求めなさい。

多边形 基础 知识讲解 安阳市网络教研平台

多边形 基础 知识讲解 安阳市网络教研平台

如果是个正五边形（所有角度相等），每个角是 540° / 5 = 108° （练习：确定每个三角形加起来是 180°，五边形加起来是 540°） 五边形内角的和是 540° 通用规则 每次加一条边（三角形到四边形，四边形到五边形等等），内角的和就增加 180° 假设是正n边形 则内角和(n2)*180=180n360 多边形外角和是360度 每一个内角比每一个外角的3倍大 一共n个角 所以内角和一共比外角和的3倍大n度 所以 180n360=3×360n 160n=1440 n=9 180n360=1260 答：这个正多边形的内角和是1260度

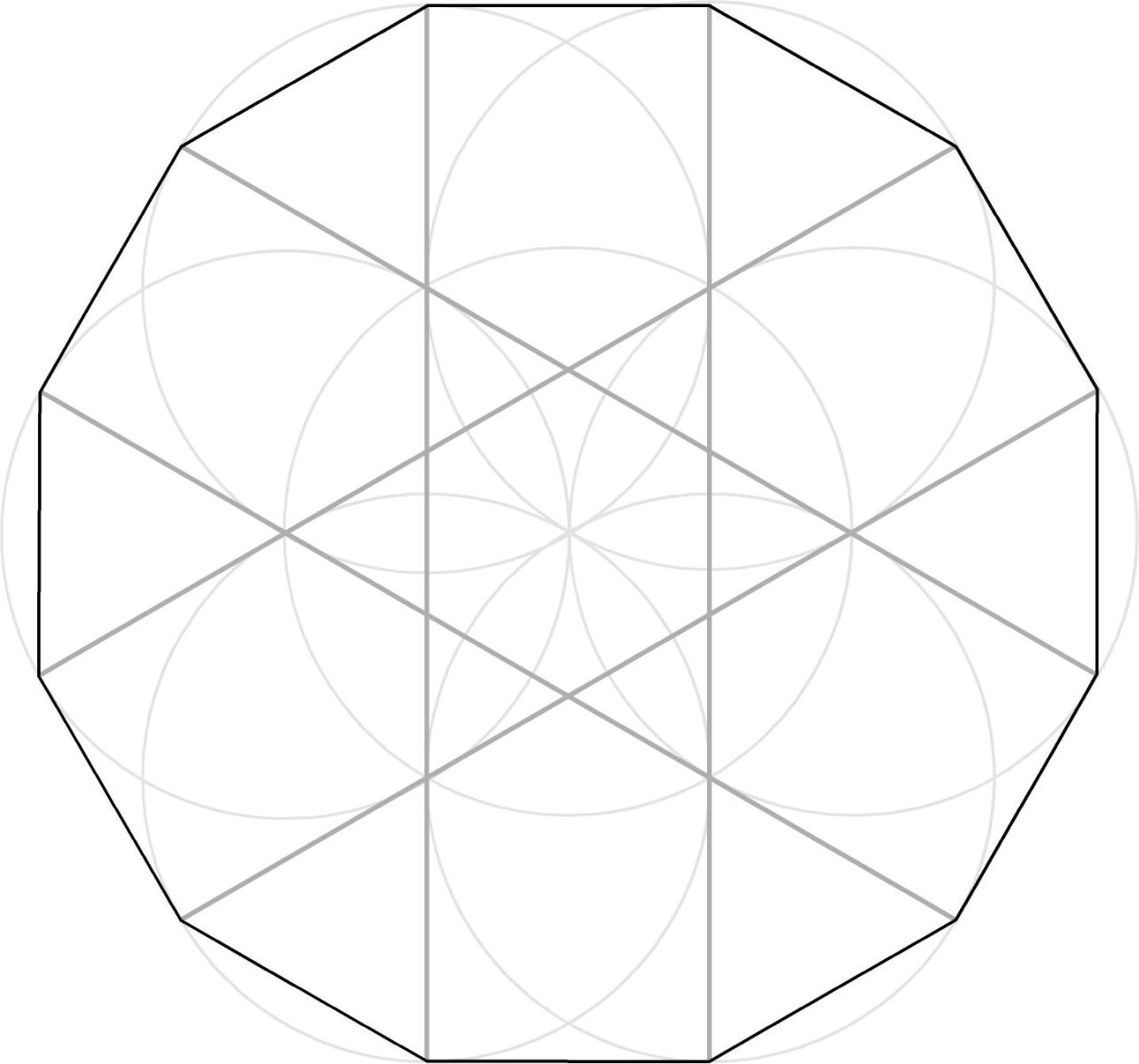
正十二边形 搜狗百科

备战22年苏科版中考数学分类精练26 正多边形与弧长 扇形面积 含答案 七七文库www 77wenku Com

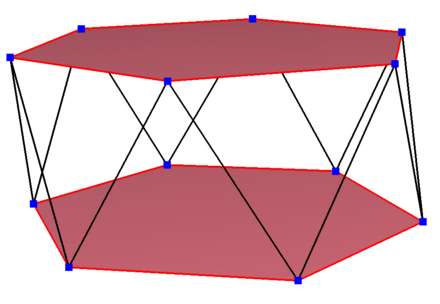
十二边形 Wikiwand

正三十二边形图片 十二边形图片 伤感说说吧

全历史

七年级数学检测 Doc 文档分享网

全历史

十二边形 维基百科 自由的百科全书

十二边形的内角和是多少度一个十二边形的内角和是多少度 天奇生活

十二边形 快懂百科

1

有趣的面积问题 六边形

正十二面体体积推导 一 知乎

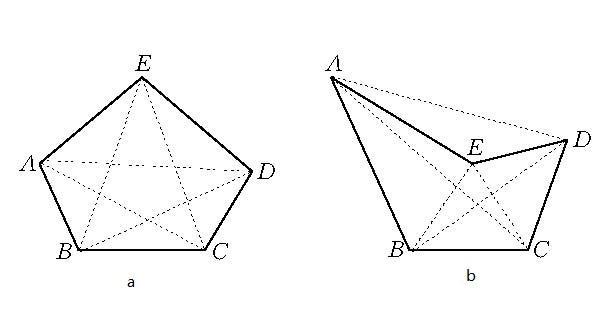
十二边形 搜狗百科

24 3正多边形和圆第1课时正多边形的判定课件21 22学年沪科版九年级数学下册 Pptx 师客文库

两种解题方法求五边形内角和 知识点需要明晰推导过程进而归纳 每日头条

多边形内角和外角 西瓜视频搜索

编程 Scratch 02 巧用scratch画正多边形 少儿编程教程网

正12边形第1页 驾考预约大全

12边形内角和 搜狗搜索

全历史

备战22年苏科版中考数学分类精练26 正多边形与弧长 扇形面积 含答案 七七文库www 77wenku Com

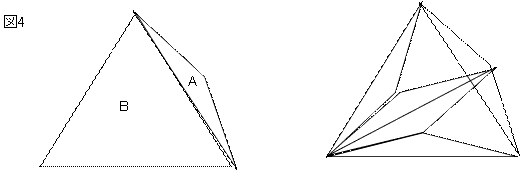
問題187 正十二角形の秘密

内角和的公式 西瓜视频搜索

初二勇数学网课7月16日part 2 Youtube

19年中考真题汇总 平行四边形的这几个题比较经典 内角 性质 对角

正12边形的每个内角是150度 为什么呢 百度知道

备战22年苏科版中考数学分类精练26 正多边形与弧长 扇形面积 含答案 七七文库www 77wenku Com

正十二边形 快懂百科

二十边形的内角和是多少 知道谷

正12角形内角 ニスヌーピー壁紙

正三十二边形图片 十二边形图片 伤感说说吧

六边形内角和一共多少度 知道谷

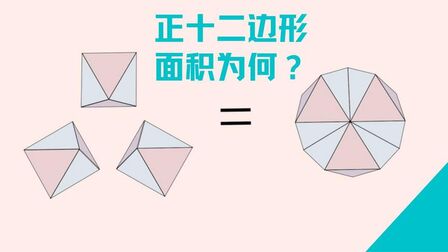
正12边形面积公式 搜狗搜索

十二边形的内角和是多少度一个十二边形的内角和是多少度 天奇生活

正五边形内角多少度 西瓜视频搜索

备战22年苏科版中考数学分类精练26 正多边形与弧长 扇形面积 含答案 七七文库www 77wenku Com

正12边形第1页 驾考预约大全

問題187 正十二角形の秘密

正多边形二十角形内角petrie多边形png图片素材免费下载 图片编号 Png素材网

この2つ教えて欲しいです 答えはそれぞれ125度と正12角形です Clearnote

正12边形第1页 驾考预约大全

五边形有几个外角正五边形外角和多少度 天奇生活

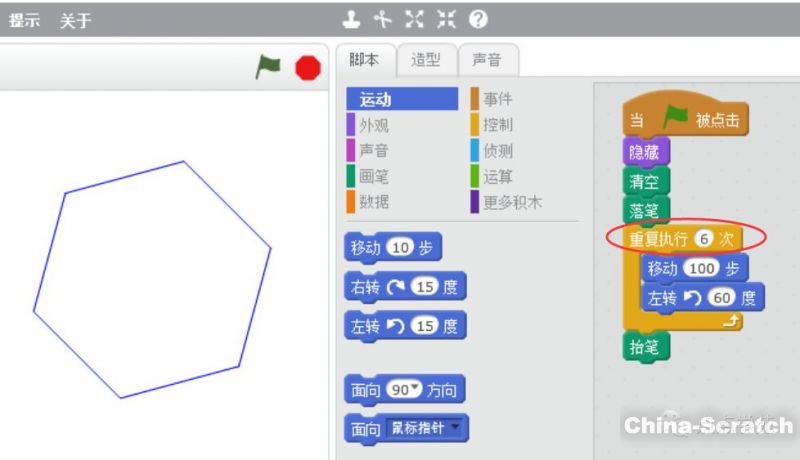
编程 Scratch 02 巧用scratch画正多边形 少儿编程教程网

五边形内角和是多少五边形的内角和怎么求 天奇生活

角二十角形十二角形交叉反棱镜多边形角png图片素材免费下载 图片编号 Png素材网

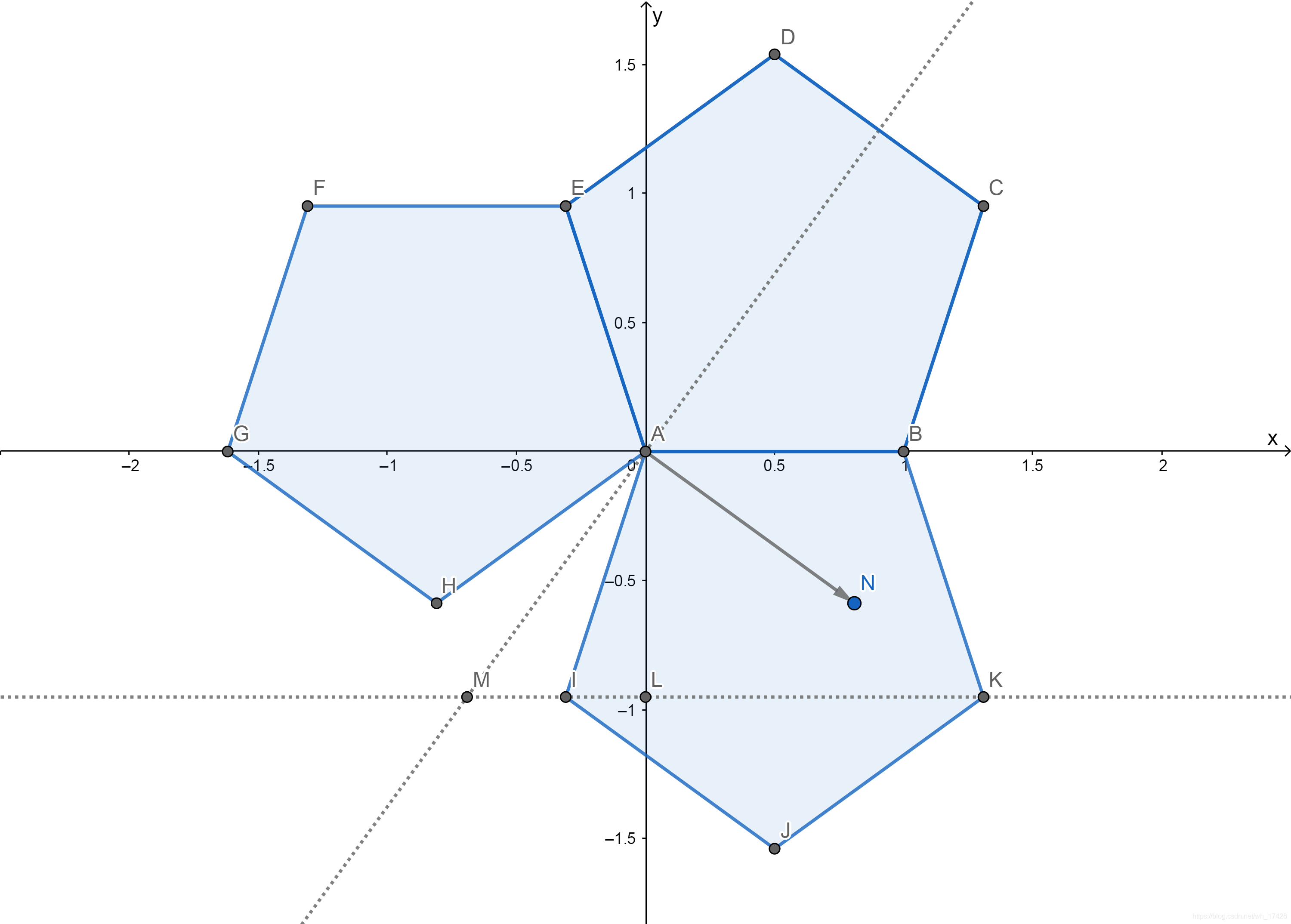
正十二面体二面角的一种求法 Wh 的博客 Csdn博客 正十二面体

湘教版八年级下 多边形的内角和 最新 沃文网wodocx Com

从正3边形到正12边形的内角和 和每一个内角的度数 院勾问答

正12边形第1页 驾考预约大全

二十边形的内角和是多少 知道谷

第4讲多边形21年新八年级数学暑假课程 华师大版 解析版 Doc 师客文库

十二角形 Wikipedia

正十二边形 快懂百科

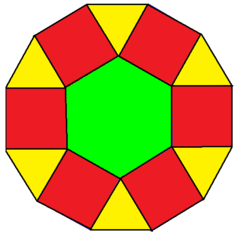
十二边形 Wikiwand

正多边形与圆 Ppt课件2下载 牛二ppt

湘教版八年级下 多边形的内角和 最新 沃文网wodocx Com

五边形每个内角多少度 五边形内角和 100教育资讯网

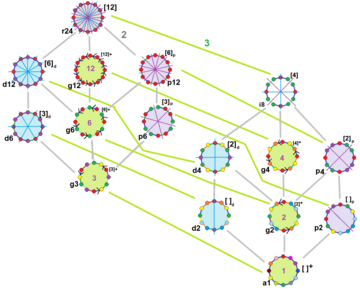
十二边形 维基百科 自由的百科全书

正5角形可以和 正3角形 或正6角铺地板吗 正6角形呢 学学习作业帮

Atcoder Agc051 A Dodecagon 解説

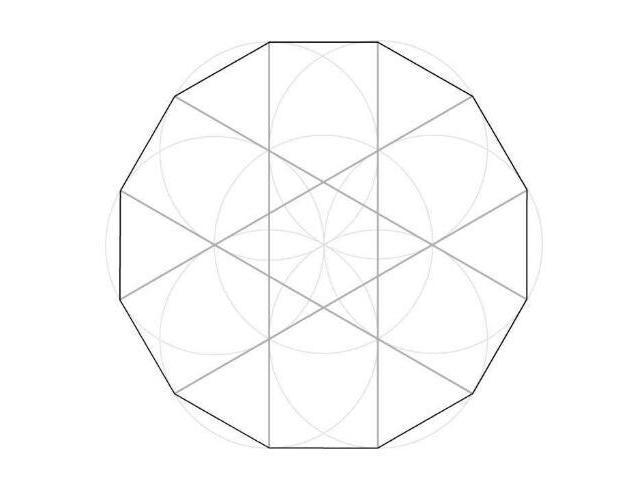
十二边形 搜狗百科

多边形的内角和 三角形ppt下载 第一ppt

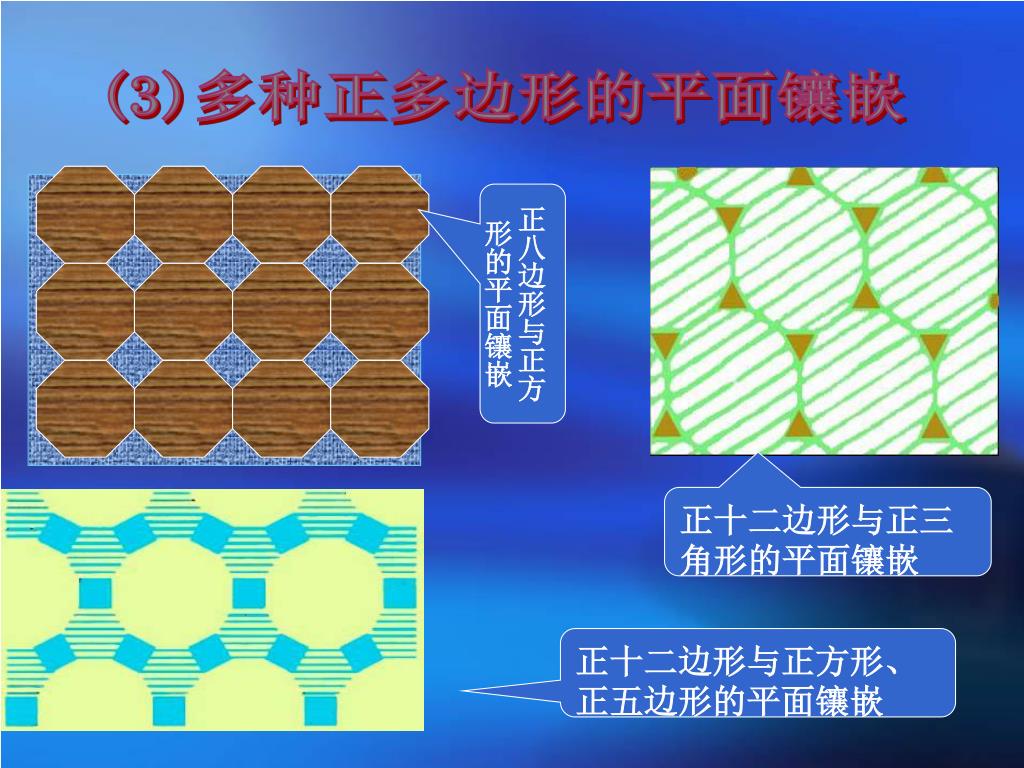
Ppt 课题学习镶嵌powerpoint Presentation Free Download Id

多边形的内角度数 西瓜视频搜索

正五边形的内角和是 时习社区

正六边形内角多少度正五边形内角多少度 问呗头条网

例題 正12 邊形的內角外角 Youtube

万花筒与正多边形满铺

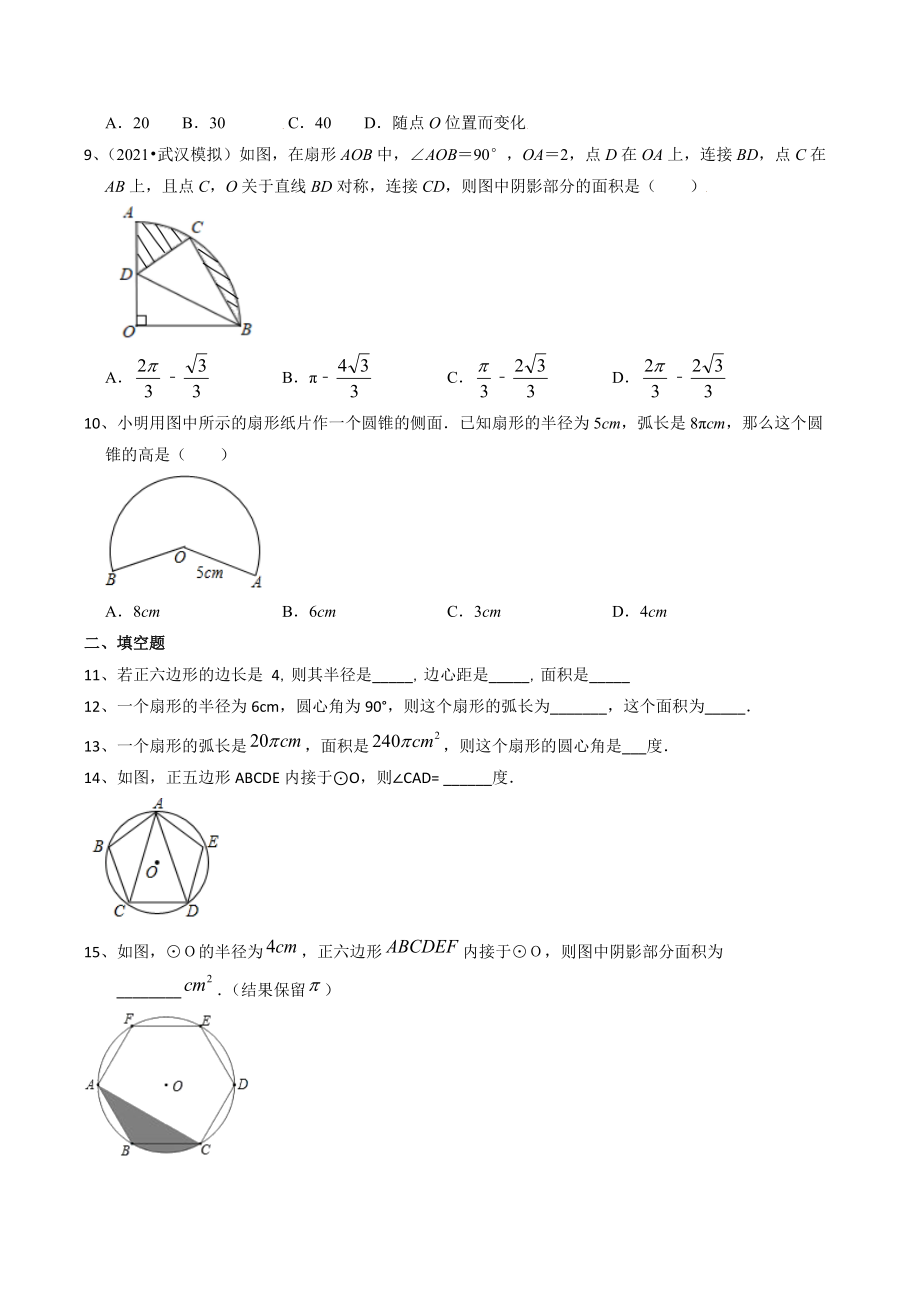
备战22年苏科版中考数学分类精练26 正多边形与弧长 扇形面积 含答案 七七文库www 77wenku Com

十二边形的内角和是多少度一个十二边形的内角和是多少度 天奇生活

正多边形十二角八角形png图片素材免费下载 图片编号 Png素材网

正12边形第1页 驾考预约大全

18年迎春杯初赛五年级每日一练 正八边形与正十二边形 迎春杯辅导 奥数网

全历史

正12角形の内角の和を求めなさい の問題を解説してくださ Yahoo 知恵袋

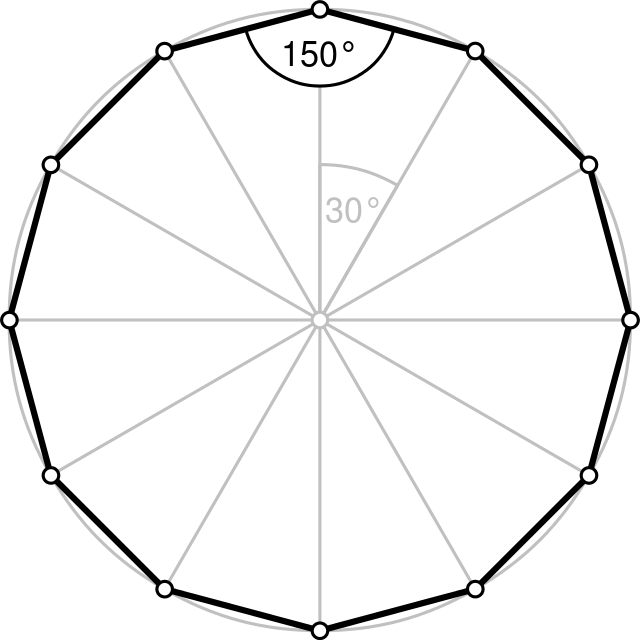
十二边形 维基百科 自由的百科全书

十二边形 Wikiwand

正多边形与圆 Ppt课件2下载 牛二ppt

十二边形 Wikiwand

星形多边形正多边形内角png图片素材免费下载 图片编号 Png素材网

正五边形abcde中 你会求 m的度数吗 陕西中考数学真题 多边形的内角和公式 外角和公式 哔哩哔哩 つロ干杯 Bilibili

有趣的面积问题 六边形

正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

正三十二边形图片 十二边形图片 伤感说说吧

Incoming Term: 正12角形 内角,